ATURAN SINUS DAN COSINUS
BAB I
PENDAHULUAN
A. LATAR BELAKANG
Pada awalnya, trigonometri disebut juga ilmu ukur segitiga atau ilmu ukur sudut yang mencoba menyelidiki gerak benda-benda angkasa seperti matarahi, bulan, dan bintang, serta memperkirakan posisinya. Trigononetri berasal dari bahasa Greek, yaitu trigon yang artinya segitiga, dan metran yang artinya ukuran. Trigonometri merupakan sebuah cabang matematika yang berhadapan dengan sudut segitiga dan fungsi trigonometrik seperti sinus, cosins, tangen.
B. RUMUSAN MASALAH
Adapun rumusan masalah dalam makalah ini:
1. Bagaimana aturan cosinus dan penjabarannya?
2. Bagaimna aturan sinus dan penjabarannya?
C. TUJUAN
Adapun tujuan dari pembahasan makalah ini yaitu:
1. Bahan bacaan siswa/i.
2. Bahan pembelajaran atau sumber belajar bagi siswa/i.
3. Untuk mengetahui bagaimana aturan sinus dan cosinus serta penjabarannya.
BAB II
PEMBAHASAN
1.
2. ATURAN COSINUS DAN PENJABARANNYA
Teorema
Pythagoras merupakan suatu rumus yang sangat penting dalam geometri. Kita dapat
menghitung jarak antara dua titik pada bidang koordinat dengan menggunakan
teorema Pythagoras. Kita juga dapat menurunkan persamaan lingkaran dengan
menggunan teorema tersebut.
Teorema Pythagoras memang sangat sering digunakan. Akan tetapi
penggunaan tersebut dibatasi hanya pada permasalahan yang melibatkan segitiga
siku-siku. Teorema Pythagoras tidak berlaku untuk segitiga lancip ataupun
segitiga tumpul. Mengapa demikian?
Apabila
sisi siku-siku dari segitiga siku-siku dibuat lebih dekat (sudut yang diapitnya
semakin kecil) maka sudut siku-sikunya akan menjadi sudut lancip, dan
diperoleh c2 < a2+ b2. Untuk membuat
pertidaksamaan ini menjadi suatu persamaan, kita perlu mengurangi a2 + b2 dengan nilai
tertentu.
c2 = a2 + b2 – nilai tertentu
Sebaliknya,
apabila sisi siku-sikunya dibuat lebih jauh (sudut yang diapitnya semakin
besar) maka sudut siku-sikunya akan menjadi sudut tumpul, dan diperoleh c2 > a2 + b2. Berikut ini persamaan yang terjadi apabila kita menambahkan
nilai tertentu pada a2 + b2.
c2 = a2 + b2 + nilai tertentu
Nilai
tertentu tersebut tak lain adalah 2ab ∙ cos C. Rumus hasil modifikasi dari teorema Pythagoras ini
disebut aturan cosinus.
Aturan Cosinus
Untuk
sembarang segitiga yang panjang sisi-sisinya a, b, dan c, serta C adalah sudut
di hadapan sisi yang panjangnya c,
c2 = a2 + b2 – 2ab ∙ cos C
Karena
nilai cos dari sudut tumpul adalah negatif, maka nilai dari 2ab ∙ cos C juga bernilai
negatif. Sehingga pengurangan oleh 2ab ∙ cos C akan sama dengan penjumlahan oleh nilai positif.
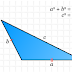
Untuk
menurunkan aturan cosinus pada segitiga lancip, perhatikan segitiga ABC dengan AD sebagai
garis tinggi, yang ditunjukkan oleh gambar di atas. Kita dapat menyebut panjang
sisi-sisi di depan sudut A, B, dan C secara
berturut-turut adalah a, b, dan c, tingginya
adalah t, serta panjang sisi CD sebagai x. Panjang dari sisi BD merupakan
hasil pengurangan panjang sisi BC oleh CD, yaitu a – x.
Dengan
menggunakan teorema Pythagoras, kita dapat menulis dua persamaan. Dengan
aljabar, kita dapat menjabarkan bentuk (a – x)2.
Perhatikan
kedua persamaan tersebut memuat x2 + t2, yang kita tahu sama dengan b2 dari persamaan 1. Substitusikan
persamaan 1 ke persamaan 2.
Sekarang
yang kita butuhkan adalah mengganti x dengan bentuk
yang memuat cos C. Dengan menggunakan
segitiga ACD, kita dapat menulis persamaan berikut dan
menuliskan x dalam bentuk cos C.
Substitusikan persamaan 4 ke persamaan 3, sehingga diperoleh
rumus aturan cosinus.
c2 = a2 + b2 – 2ab cos C
Walaupun
penurunan aturan cosinus ini dilakukan pada segitiga lancip, aturan ini juga
berlaku pada segitiga tumpul. Kita dapat menggunakan aturan cosinus apabila
diketahui panjang 3 sisi segitiga atau panjang dua sisi segitiga dan besar
sudut yang diapitnya (ss.ss.ss atau ss.sd.ss).
Aturan Sinus
Dalam trigonometri, aturan sinus, rumus sinus, atau hukum sinus adalah sebuah persamaan yang memperbandingan panjang sisi-sisi segitiga terhadap sinus sudut-sudutnya. Aturan ini menyatakan bahwa


Aturan sinus adalah salah satu dari dua persamaan trigonometrik yang umum digunakan untuk menentukan besar panjang dan sudut pada segitiga, persamaan lain yang digunakan adalah aturan kosinus.
Aturan sinus dapat diperumum ke dimensi yang lebih tinggi, yakni pada permukaan dengan kurvatur yang bernilai konstan
Pembuktian:
Perhatikan segitiga dengan sisi a, b, dan c, dan sudut yang berhadapan A, B, dan C. Tarik garis tinggi h dari sudut C ke sisi c sehingga segitiga ABC terbagi menjadi dua segitiga siku-siku.
Dapat diamati bahwa:
 dan
dan
Dari persamaan tersebut, dapat diturunkan dua bentuk dari h

sehingga diperoleh

Memperlakukan garis tinggi dari sudut A dengan cara yang sama, kemudian akan diperoleh:

BAB III
PENUTUP
A. KESIMPILAN
Hukum cosinus, atau disebut juga aturan cosinus, dalam trigonometri adalah aturan yang memberikan hubungan yang berlaku dalam suatu segitiga, yaitu antara panjang sisi-sisi segitiga dan cosinus dari salah satu sudut dalam segitiga tersebut. Sedangkan Hukum sinus ialah pernyataan tentang segitiga yang berubah-ubah di udara. Jika sisi segitiga ialah (kasus sederhana) a, b dan c dan sudut yang berhadapan bersisi (huruf besar) A, B and C. B. SARAN
Alhamdulillah segala puji syukur penulis panjatkan kepada Allah AWT, atas rahmatnya dan hidayahnya yang telah memberikan kesempatan untuk kami sehingga kami bisa menulis makalah ini, dan dengan kekurangan-kekurangan yang ada pada penulisan maka dari itu saya mengharap saran dan kritik untuk menuju kepada yang lebih baik.
Penulis menyarankan kepada para pembaca agar lebih baik memahami tentanga penjabaran aturan Cosinus dan Sinus dalam identitas Trigonometri Ungkapan terimakasih kepada Dosen mata kuliah Trigonometri sehingga terselesainya tulisan ini. Mudah-mudahan Allah SWT meridhoi apa yang kita kerjakan. Amin. Demikianlah makalah singkat ini kami buat semoga bisa bermanfaat bagi kita semua, namun dalam penulisan ini masih banyak kesalahan, tapi bagaimanapun juga ini adalah langkah awal bagi kami atau pengalaman bagi kami untuk menulis makalah ini. Dan atas perhatian pembaca kami ucapkan terimakasih dan kami akhiri wassalam
ATURAN SINUS DAN COSINUS LENGKAP BESERTA PEMBUKTIAN SEMOGA BERMANFAAT







m.jpg)